y=sinx ֆունկցիայի հատկությունները

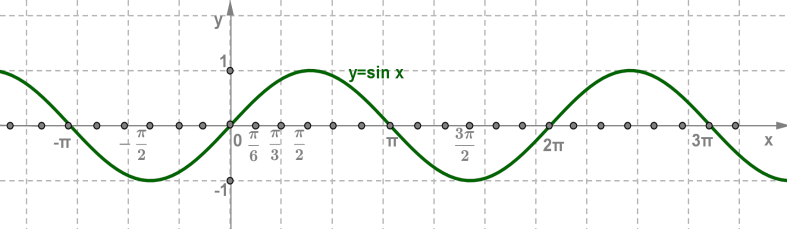
1. y=sinx ֆունկցիայի որոշման տիրույթն ամբողջ թվային առանցքն է՝ D(sinx)=R:

2. y=sinx ֆունկցիայի արժեքների բազմությունը [−1;1] հատվածն է:

3. y=sinx ֆունկցիան պարբերական է T=2π պարբերությամբ: 

4. y=sinx ֆունկցիան կենտ է:

5. sinx=0, երբ x=πn,n∈Z: 

6. y=sinx ֆունկցիայի մեծագույն արժեքը 1-ն է, որը ֆունկցիան ընդունում է x=π2+2πn,n∈Z կետերում: 

7. y=sinx ֆունկցիայի փոքրագույն արժեքը −1-ն է, որը ֆունկցիան ընդունում է x=−π2+2πn,n∈Z կետերում:

8. y=sinx ֆունկցիան դրական է (2πn;π+2πn) արգումենտների համար, և բացասական է

(π+2πn;2π+2πn) արգումենտների համար, որտեղ n∈Z:

9. y=sinx ֆունկցիան աճում է [−π2+2πn;π2+2πn] հատվածներում և նվազում է [π2+2πn;3π2+2πn] հատվածներում, որտեղ n∈Z:

Հաշվի առնելով թվարկված հատկությունները, կառուցում ենք y=sinx ֆունկցիայի գրաֆիկը:

Ուղղանկյուն եռանկյան սուր անկյան տանգենսը և կոտանգենսը սահմանվում են հետևյալ կերպ՝

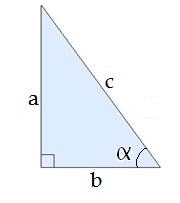tgα=դիմացի էջկից էջtgα=abctgα=կից էջդիմացի էջctgα=ba

Տանգենսի արժեքը ստանալու համար պետք է միավոր շրջանագծին շոշափող տանել (1;0) կետում:Տանգենսի արժեքները գտնվում են Oy առանցքի վրա: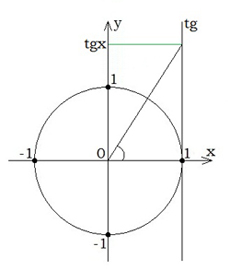
Կոտանգենսի արժեքը ստանալու համար պետք է միավոր շրջանագծին շոշափող տանել (0;1) կետում:Կոտանգենսի արժեքները գտնվում են Ox առանցքի վրա: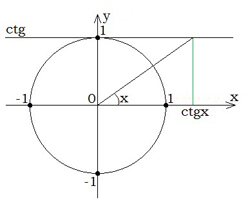

Տանգենսի և կոտանգենսի արժեքները հաշվում ենք արդեն ծանոթ բանաձևերի միջոցով՝

tgα=sinαcosαctgα=cosαsinα

Կարևոր է հիշել տանգենսի և կոտանգենսի հետևյալ արժեքները:

tg0°=0tg90°  գոյություն չունիtg180°=0tg270° գոյություն չունիtg360°=0

ctg0° գոյություն չունիctg90°=0ctg180° գոյություն չունիctg270°=0ctg360° գոյություն չունի

Եռանկյունաչափական ֆունկցիաների հետևյալ արժեքները պետք է անգիր իմանալ:

	30°	45°	60°
sinα	12	2−−√2	3−−√2
cosα	3−−√2	2−−√2	12
tgα	3−−√3	1	3−−√
ctgα	3−−√	1	3−−√3

Ցանկացած α անկյան համար տեղի ունեն հետևյալ բանաձևերը՝

tg(−α)=−tgα,ctg(−α)=−ctgα: