Առարկայի պատկերի կառուցումը բարակ ոսպնյակում

Տարբեր օպտիկական սարքերում կիրառվող ոսպնյակները թույլ են տալիս ոչ միայն հավաքել կամ ցրել լուսային ճառագայթները, այլև ստանալ առարկաների զանազան՝ մեծացած կամ փոքրացած, ուղիղ կամ շրջված, իրական կամ կեղծ պատկերները:

Ստացված պատկերի բնույթը կախված է ոսպնյակի տեսակից, ինչպես նաև առարկայի և ոսպնյակի փոխդասավորությունից:

Եթե լուսատու կամ լուսավորվաշ առարկայի որևէ S կետից արձակվող 2 կամ ավելի ճառագայթներ ոսպնյակով անցնելուց հետո հատվում են որոշակի  S¹ կետում,ապա այդ պատկերն անվանում են S կետի իրական պատկեր:Եթե S կետից ելնող տարամետ ճառագայթները ոսպնյակում բեկվելուց հետո դարձյալ տարանիտում են ,բայց շարունակությունները հատվում են որոշակի S¹ կետում ,ապա S¹-ը կոչվում է S կեստի կեղծ պատկերը:

Առարկայի պատկերը ստանալու համար կարիք չկա ստանալ նրա բոլոր կետերի պատկերները. բավական է կառուցել առարկայի ծայրակետերի պատկերը: Առարկայի պատկերը ընկած կլինի նրանց միջև: Իսկ ծայրակետի պատկերը ստանալու համար կարելի է ընտրել այդ կետից դուրս եկող անհամար ճառագայթներից այն երկուսը, որոնց ընթացքը ոսպնյակում նախօրոք հայտնի է:

Այդպիսի «հարմար» ճառագայթներն են.

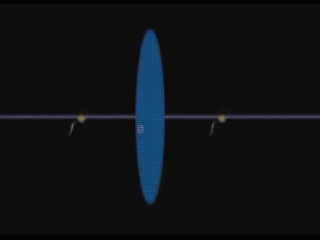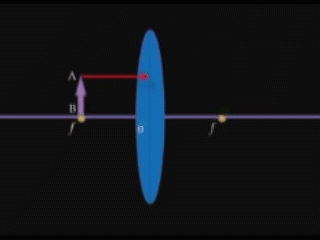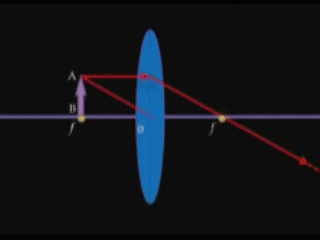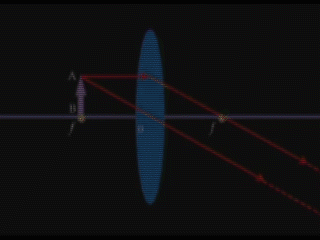
ա) ոսպնյակի օպտիկական կենտրոնով անցնող ճառագայթը.

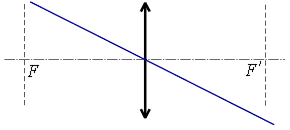
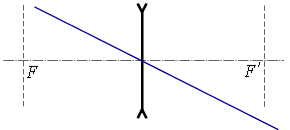
Ոսպնյակով անցնելիս այս ճառագայթը չի փոխում իր ուղղությունը:

բ) ոսպնյակի գլխավոր օպտիկական առանցքին զուգահեռ ճառագայթը.

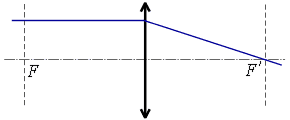
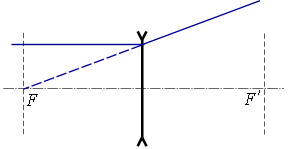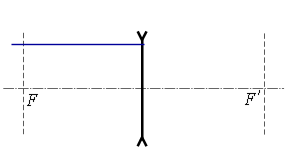
Ոսպնյակով անցնելիս, եթե ոսպնյակը հավքող է՝ ապա ճառագայթը, իսկ եթե ցրող է՝ ճառագայթի շարունակությունը, անցնում է ոսպնյակի գլխավոր կիզակետով:

Օգտվելով այս «հարմար» ճառագայթներից, օրինակ, կարող ենք կառուցել AB մատիտի պատկերը, եթե ստանանք նրա A և B ծայրակետերի պատկերները՝ A1-ը և B1 -ը: A1B1 հատվածը կլինի AB մատիտի պատկերը

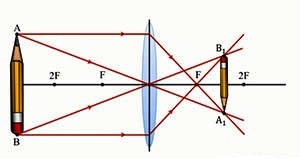
Նշանակենք առարկայի հեռավորությունը բարակ ոսպնյակից՝ d-ով, նրա պատկերի հեռավորությունը ոսպնյակից՝f-ով, իսկ ոսպնյակի կիզակետային հեռավորությունը՝ F-ով և դիտարկենք հետևյալ դեպքերը.

d>>F /առարկան շատ հեռու է ոսպնյակից/

Այսպիսի առարկաներ են օրինակ Արեգակը,աստղերը:Շատ հեռու առարկայից եկող ճառագայթները,որոնք ընկնում են ոսպնյակի վրա ,գրեթե զուգահեռ են :Ուստի այդ առարկնաերը հավաքող ոսպնյակում պատկերում են կիզկետում՝ լուսավոր,փոքր կետի տեսքով:

Առարկան կրկնակի կիզկետից դուրս է d>2F

Առարկան պատկերել դեպի վեր ուղղավծ ուղղաձիգ սլաքի տեսքով:Ենթադրենք այն ոսպնյակի ձախ կողմում է : Կառուցումով համոզվում ենք,որ առարկայի իրական պատկերը ոսպնյակից աջ է ՝  F  և 2F կետերի միջև,շրջված է ,փոքրացած

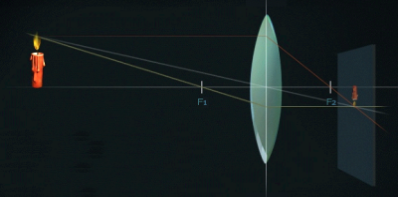
3. d=2F /առարկան տեղադրված է ոսպնյակից՝ նրա կրկնակի կիզակետային հեռավորության վրա/

Կառուցումից երևում է, որ առարկայի պատկերը իրական է, շրջված, նույն չափերի՝ H=h  և ոսպնյակից նույն հեռավորության վրա՝ d=2F:

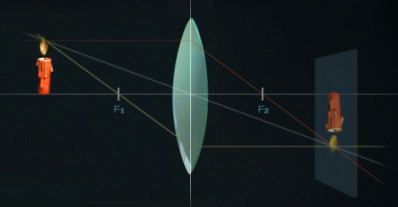
4. F<d<2F /առարկան տեղադրված է ոսպնյակի կիզակետի և կրկնակի կիզակետի միջև/

Կառուցումից երևում է, որ սլաքի պատկերը իրական է, շրջված, մեծացած՝ H>h և ոսպնյակի կրկնակի կիզակետային հեռավորությունից մեծ հեռավորության վրա՝ f>2F

5. d=F /առարկան տեղադրված է ոսպնյակի գլխավոր կիզակետում/

Կառուցումից երևում է, որ սլաքի ծայրակետերից դուրս եկող ճառագայթները ոսպնյակում բեկվելուց հետո դառնում են իրար զուգահեռ, հետևաբար չեն հատվում և պատկեր չի ստացվում:

6. 0<d<F /առարկան տեղադրված է ոսպնյակի և նրա կիզակետի միջև/

Կառուցումից երևում է, որ սլաքի պատկերը ստացվում է կեղծ, ուղիղ, մեծացած՝ H>h, ոսպնյակի նույն կողմում, որտեղ առարկան է:

Կատարելով նույնանման կառուցումներ, կստանանք, որ առարկայի պատկերը ցրող ոսպնյակում` անկախ առարկայի դիրքից, կեղծ է, փոքրացած, ուղիղ և ոսպնյակի նույն կողմում, որտեղ առարկան է:

Ոսպնյակից առարկայի պատկերի f հեռավորությունը կարելի է որոշել նաև առանց կառուցման: Դրա համար բավական է իմանալ առարկայի d հեռավորությունը և ոսպնյակի F կիզակետային հեռավորությունը: Այդ 3 մեծությունները իրար հետ կապված են 1/F=1/d+1/f հավասարմամբ, որն անվանում են բարակ ոսպնյակի բանաձև:Այս բանաձևը նւոյնպես հնարավորություն է տալիս որոշել պատկերի կամայական դիրքի հեռավորությունը ոսպնյակից : Մասնավորապես, եթե առարկան կրկնակի կիզկետում է (d=2F) ապա ստանում ենք  f=2F:Կառուցման միջոցով պարզեցինք ,որ պատկերի չափն առարկայի չափից կարող է լինել մեծ,նույն չափի  կամ փոքր: Պատկերի ՝ առարկայի համեմատությամբ մեծ կամ փոքր չափը բնութագրվում է մի հարաբերական մեծությամբ,որը կոչվում է ոսպնյակի խոշորացում  և հավասար է պատկերի և առարկայի համապատասխան գծային չափերի հարաբերությանը:

Եթե ոսպնյակի խոշորացումը նշանակենք  Г գամմա տառով,իսկ առարկայի և պատկերի գծային չափը h-ով և h¹-ով,

ապա ըստ սահմանման Г=h¹/h

Համաձայն հաշվարկների Г=f/d

1.Որոշեք ցրող ոսպնյակի օպտիկական ուժը, եթե նրա կեղծ կիզակետը գտնվում է ոսպնյակից 200 սմ հեռավորության վրա:  

D=1/F

1/200=1/2=0,5

2. Ոսպնյակի օպտիկական ուժը 2 դպտր է: Ինչպիսի՞ ոսպնյակ է այն՝ հավաքող, թե՞ ցրող: Որքա՞ն է նրա կիզակետային հեռավորությունը:

Ոսպնյակը հավաքող է քանի որ դպտր-ի միավորը դրական է: Կիզակետային հեռավորությունը F=1 ․ D=1 . 2=2

3.Ինչպիսի՞ն է ապակե երկգոգավոր ոսպնյակը:

 ա.  ցրող

բ. իրական

գ. կեղծ

դ. հավաքող

4.Ինչպե՞ս է կոչվում այն կետը, որում ոսպնյակում բեկվելուց հետո հավաքվում են հավաքող ոսպնյակի գլխավոր օպտիկական առանցքին զուգահեռ ճառագայթները:

Այդ կետը կոչվում է Գլխավոր կիզակետ:

5. Առարկայի բարձրությունը 70 սմ է, իսկ նրա պատկերի բարձրությունը 52 սմ: Որքա՞ն է ոսպնյակի գծային խոշորացումը:

Г=H/h=70/52=1,3

6.Որքա՞ն է 0.8 մետր բարձրությամբ առարկայի պատկերի բարձրությունը, եթե ոսպնյակի գծային խոշորացումը 2.5 է: Պատասխանը գրել տասնորդականի ճշտությամբ:

H=Г . h=0,8 . 2,5=2մ